Clustering algorithms represent fundamental unsupervised learning techniques that automatically discover hidden patterns within data. Unlike supervised learning methods, these algorithms work without labeled examples, making them invaluable for exploratory data analysis and pattern recognition tasks.
Data scientists and machine learning practitioners rely on clustering algorithms to segment customers, organize documents, detect anomalies, and uncover meaningful structures in complex datasets. Consequently, understanding these techniques becomes essential for anyone working with unlabeled data or seeking to extract insights from large information repositories.
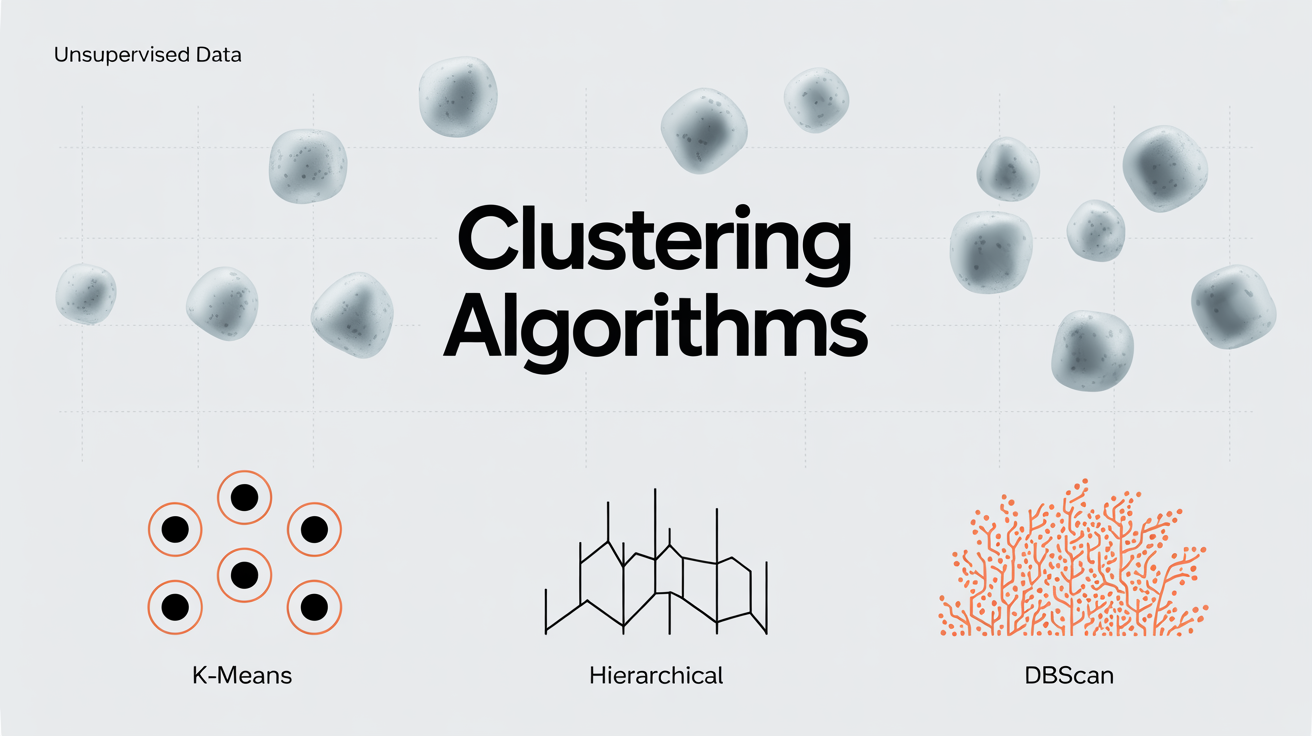
K-Means Clustering: Algorithm and Implementation
K-means clustering stands as one of the most widely adopted clustering algorithms due to its simplicity and effectiveness. The algorithm partitions data into k clusters by minimizing the within-cluster sum of squares, creating compact and well-separated groups.
The K-means process begins by randomly initializing k cluster centroids in the feature space. Subsequently, each data point gets assigned to the nearest centroid based on Euclidean distance. The algorithm then recalculates centroid positions as the mean of all assigned points, repeating this process until convergence occurs.
Key advantages of K-means include:
- Computational efficiency for large datasets
- Simple implementation and interpretation
- Guaranteed convergence to local optimum
However, the algorithm has notable limitations. K-means assumes spherical clusters and requires predefined cluster numbers. Additionally, it struggles with varying cluster sizes and densities, making it unsuitable for complex data distributions.
Implementation considerations involve proper data preprocessing, including feature scaling and handling categorical variables. The scikit-learn library provides robust K-means implementations with various initialization strategies and convergence criteria.
Hierarchical Clustering: Agglomerative and Divisive Methods
Hierarchical clustering creates tree-like structures called dendrograms that reveal data relationships at multiple granularity levels. This approach eliminates the need for predetermined cluster numbers while providing insights into data hierarchy and natural groupings.
Agglomerative clustering follows a bottom-up approach, starting with individual data points as separate clusters. The algorithm iteratively merges the closest cluster pairs based on linkage criteria such as single, complete, or average linkage. This process continues until all points belong to a single cluster, creating a comprehensive dendrogram.
Conversely, divisive clustering employs a top-down strategy, beginning with all data points in one cluster. The method recursively splits clusters until each point forms its own group. Although theoretically appealing, divisive methods are computationally expensive and less commonly used in practice.
Linkage criteria significantly impact clustering results:
- Single linkage connects clusters based on minimum pairwise distance
- Complete linkage uses maximum pairwise distance
- Average linkage considers mean distance between all point pairs
The primary advantage of hierarchical clustering lies in its ability to reveal data structure at various scales. Furthermore, the method produces deterministic results without requiring random initialization. However, the approach suffers from high computational complexity, making it unsuitable for extremely large datasets.
Research from MIT’s Computer Science department demonstrates that hierarchical clustering excels in biological data analysis, particularly for gene expression studies and phylogenetic tree construction.
Density-Based Clustering: DBSCAN and OPTICS
Density-based clustering algorithms identify clusters as regions of high data density separated by areas of low density. These methods excel at discovering arbitrary-shaped clusters while automatically detecting outliers as noise points.
DBSCAN (Density-Based Spatial Clustering of Applications with Noise) represents the most popular density-based algorithm. The method defines clusters as dense regions containing at least a minimum number of points within a specified radius. Core points have sufficient neighbors within the radius, while border points lie within the neighborhood of core points but lack sufficient neighbors themselves.
The algorithm requires two parameters: epsilon (neighborhood radius) and minimum points for core point classification. DBSCAN groups core points and their reachable neighbors into clusters, marking isolated points as noise. This approach naturally handles varying cluster shapes and sizes while identifying outliers.
DBSCAN advantages include:
- Automatic noise detection and outlier identification
- No need to specify cluster numbers beforehand
- Robust handling of arbitrary cluster shapes
OPTICS (Ordering Points To Identify the Clustering Structure) extends DBSCAN by addressing parameter sensitivity issues. Instead of producing explicit clusters, OPTICS generates a reachability plot that reveals clustering structure across different density levels. This approach provides more flexibility in cluster extraction and parameter selection.
Studies published by Stanford’s AI Research Institute show that density-based methods outperform traditional clustering approaches for spatial data analysis and anomaly detection tasks.
Clustering Validation: Silhouette Score, Elbow Method, Gap Statistic
Clustering validation measures help assess cluster quality and determine optimal algorithmic parameters. These metrics provide objective criteria for comparing different clustering solutions and selecting the most appropriate approach for specific datasets.
The silhouette score measures how similar points are to their own cluster compared to other clusters. Values range from -1 to 1, where higher scores indicate better-defined clusters. For each point, the metric calculates the mean distance to same-cluster points and the mean distance to nearest-cluster points, providing both global and individual cluster quality assessments.
The elbow method analyzes within-cluster sum of squares across different cluster numbers. Plotting these values typically reveals an “elbow” point where additional clusters provide diminishing returns. This heuristic helps identify optimal cluster numbers, though the elbow may not always be clearly defined.
The gap statistic compares clustering results with random data distributions:
- Calculates within-cluster dispersion for actual data
- Compares results with randomly generated reference datasets
- Identifies cluster numbers where actual data shows significantly more structure than random data
Additionally, the Davies-Bouldin index measures average similarity between clusters, with lower values indicating better separation. The Calinski-Harabasz index evaluates cluster separation and compactness, providing another perspective on clustering quality.
Research from Carnegie Mellon’s Machine Learning Department emphasizes the importance of using multiple validation metrics, as different measures may favor different clustering characteristics.
Choosing Optimal Number of Clusters
Determining the optimal number of clusters remains one of clustering’s most challenging aspects. Multiple approaches exist, each with specific strengths and limitations depending on data characteristics and clustering objectives.
The elbow method examines how clustering cost decreases as cluster numbers increase. Typically, cost reduction slows significantly after the optimal number, creating an elbow-shaped curve. However, this approach may fail when elbows are not pronounced or multiple potential elbows exist.
Information criteria such as Akaike Information Criterion (AIC) and Bayesian Information Criterion (BIC) balance clustering quality with model complexity. These methods penalize excessive cluster numbers, helping prevent overfitting while maintaining good data representation.
Cross-validation techniques provide robust cluster number selection:
- Split data into training and validation sets
- Apply clustering to training data with various cluster numbers
- Evaluate clustering quality on validation data
- Select cluster numbers that generalize well to unseen data
The gap statistic offers a principled statistical approach by comparing clustering results with null reference distributions. This method identifies cluster numbers where data shows significantly more structure than random arrangements.
Domain knowledge often provides valuable guidance for cluster number selection. Understanding the underlying problem context helps interpret validation metrics and make informed decisions about appropriate granularity levels.
Research conducted at UC Berkeley’s Statistics Department suggests combining multiple selection criteria rather than relying on single metrics, as different approaches may highlight different aspects of cluster structure.
Advanced Considerations and Best Practices
Modern clustering applications often require sophisticated preprocessing and algorithm selection strategies. Feature scaling becomes crucial when variables have different units or scales, as distance-based algorithms may be dominated by high-magnitude features.
Dimensionality reduction techniques such as Principal Component Analysis (PCA) can improve clustering performance by reducing noise and computational complexity. However, practitioners must balance dimensionality reduction benefits with potential information loss.
Ensemble clustering methods combine multiple clustering solutions:
- Run different algorithms or parameter settings
- Combine results through voting or consensus mechanisms
- Achieve more robust and stable clustering outcomes
The choice between different clustering paradigms depends on data characteristics and analytical objectives. K-means works well for spherical, similarly-sized clusters, while hierarchical methods excel when cluster relationships matter. Density-based approaches handle arbitrary shapes and noise effectively.
Recent advances in deep learning clustering integrate neural networks with traditional clustering objectives, enabling more sophisticated pattern discovery in high-dimensional spaces.
Practical Implementation Guidelines
Successful implementation of clustering algorithms requires careful attention to data preparation, algorithm selection, and result interpretation. Begin by exploring data distributions, identifying outliers, and understanding feature relationships through visualization techniques.
Clustering algorithm selection should consider dataset characteristics including size, dimensionality, expected cluster shapes, and noise levels. Large datasets may require efficient clustering algorithms like K-means or mini-batch variants, while small datasets can leverage more computationally intensive methods.
Parameter tuning plays a critical role in the success of clustering algorithms. Use validation metrics and domain knowledge to guide parameter selection, considering multiple criteria rather than optimizing single measures. Additionally, test algorithm sensitivity to parameter changes and initialization strategies.
Result interpretation involves multiple perspectives:
- Statistical validation through quantitative metrics
- Visual exploration using dimensionality reduction
- Domain expertise for semantic cluster evaluation
- Business relevance assessment for practical applications
Documentation and reproducibility become essential for production clustering systems. Record preprocessing steps, algorithm parameters, and validation criteria to ensure consistent results and enable future improvements.
Studies from Google’s Research Division demonstrate that systematic experimentation and careful validation lead to more reliable clustering outcomes in real-world applications.
FAQs:
- What is the main difference between supervised and unsupervised clustering?
Supervised learning uses labeled training data to learn patterns, while unsupervised clustering discovers hidden structures in unlabeled data without predefined categories or target variables. - How do I choose between K-means and hierarchical clustering?
K-means works best for spherical clusters of similar sizes with known cluster numbers, while hierarchical clustering excels when you need to explore data structure at multiple levels without predetermined cluster counts. - Can clustering algorithms handle categorical data?
Traditional distance-based algorithms like K-means struggle with categorical data. Use specialized methods like K-modes for categorical data or convert categories to numerical representations through encoding techniques. - What should I do if my clusters overlap significantly?
Overlapping clusters suggest fuzzy boundaries that hard clustering methods cannot capture well. Consider fuzzy clustering algorithms, mixture models, or soft clustering approaches that assign probability distributions rather than discrete cluster memberships. - How can I validate clustering results without ground truth labels?
Use internal validation metrics like silhouette score, Calinski-Harabasz index, or Davies-Bouldin index. Additionally, employ visual inspection, domain expertise, and stability analysis across multiple algorithm runs. - Is it possible to cluster high-dimensional data effectively?
High-dimensional data suffers from the curse of dimensionality, where distance measures become less meaningful. Apply dimensionality reduction techniques first, or use specialized algorithms designed for high-dimensional spaces. - What preprocessing steps are essential for clustering success?
Essential preprocessing includes feature scaling, outlier detection and handling, missing value imputation, and feature selection. Additionally, consider data transformation techniques to improve cluster separability and algorithm performance.
Stay updated with our latest articles on https://fxis.ai/