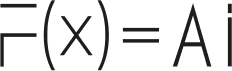If you’re delving into polynomial equations and wish to find out how many distinct integer roots exist for a specific polynomial, this blog post is for you! We’ll guide you through the calculations needed to find the constant \( k \) in the polynomial \( x^2 + kx + 36 \) that results in two distinct integer roots.

The Problem

We need to determine for how many values of the constant \( k \) the polynomial \( x^2 + kx + 36 \) has two distinct integer roots. The methodology involves using Vieta’s formulas and determining various integer pairs that produce the desired outcome.

Step-by-Step Solution

1. Introduce the roots: Let’s denote the roots of the polynomial as \( r_1 \) and \( r_2 \).
2. Apply Vieta’s Formulas: From Vieta’s, we know that:
   • The sum of the roots, \( r_1 + r_2 = -k \).
   • The product of the roots, \( r_1 \cdot r_2 = 36 \).
3. Identify Distinct Integer Pairs: We need to find all pairs \( (r_1, r_2) \) such that their product equals 36 and that \( r_1 \neq r_2 \).
4. Compute Values of \( k \): For each valid pair \( (r_1, r_2) \), we compute the corresponding value of \( k \) using the relation \( k = -(r_1 + r_2) \).
5. Ensure Distinction: Finally, we confirm that \( r_1 \) and \( r_2 \) are distinct.

Putting the Plan into Action

Now, let’s break it down further using an analogy. Imagine we are organizing two separate teams for a trivia night, each needing to sum their total knowledge points to 36. The teams cannot have the same score; they must be distinct players with unique abilities contributing to the game.

To find all possible combinations of team scores (roots) that add up to 36 while being distinct, we’d have to list out all factor pairs of 36:

# Finds all pairs (r1, r2) such that r1 * r2 = 36
product_36 = 36
factor_pairs = []

for i in range(1, product_36 + 1):
    if product_36 % i == 0:
        pair = (i, product_36 // i)
        if pair[0] != pair[1]:  # Ensure distinct pairs
            factor_pairs.append(pair)

# Calculate k for each pair and ensure distinct integer roots
valid_k_values = set()
for r1, r2 in factor_pairs:
    if r1 != r2:
        k = -(r1 + r2)
        valid_k_values.add(k)

print((len(valid_k_values), sorted(valid_k_values)))

This code snippet essentially plays the role of listing potential teams (roots) and their total skills (values of \( k \)). By the end, we find that the distinct values of \( k \) are \( -37, -20, -15, \) and \( -13 \). Thus, there are 4 valid values of \( k \) that will give us two distinct integer roots.

Output

The distinct integer values of \( k \) that result in two distinct integer roots for our polynomial are:

\[ \boxed{4} \]

Troubleshooting

If you run into issues executing the code or understanding how to find other roots, keep the following in mind:

• Ensure you’re using the correct libraries in Python (like itertools, if utilized).
• Double-check the mathematics behind Vieta’s formulas to ensure you’re accurately capturing the relationships between the roots.
• If you’re unfamiliar with Python execution, consider setting up a virtual environment or using an online Python interpreter.

For more insights, updates, or to collaborate on AI development projects, stay connected with fxis.ai.

Conclusion

By understanding how to work with polynomial root relationships and utilizing Python coding, we can uncover different constants that shape our equations. At fxis.ai, we believe that such advancements are crucial for the future of AI, as they enable more comprehensive and effective solutions. Our team is continually exploring new methodologies to push the envelope in artificial intelligence, ensuring that our clients benefit from the latest technological innovations.