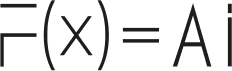Welcome to a new realm of geometry theorem proving! With the advancements in artificial intelligence and deep learning, we can now tackle complex geometry Olympiad problems without the need for human demonstrations. This guide will help you set up and get started with the DDAR and AlphaGeometry theorem provers.

What You Need

• Weight files for DDAR and AlphaGeometry
• Basic understanding of geometry and theorem proving concepts
• A compatible programming environment (Python recommended)

Getting Started

To kick-off your geometric endeavors, follow these steps:

• Clone the repository that contains the necessary weight files. You can access it using the command:

git clone https://github.com/google-deepmind/alphageometry

• Navigate to the cloned repository directory:

cd alphageometry

• Download the weight files you require from the provided sources.

An Analogy to Understand the Code

Imagine you’re an architect drawing up blueprints for a complex building. Just like you need different tools to work on different parts of the project (like a ruler for straight lines and a compass for curves), developers use various components to tackle complex geometry problems in code. The neural network components in DDAR and AlphaGeometry are akin to these tools, as they analyze and deduce theorems from various geometric elements.

Using DDAR and AlphaGeometry

After setting up the environment, here’s how you can employ these geometry provers:

• Use the command line interface to input your geometric problems.
• The theorem provers will analyze the problem using the weight files and provide potential proofs or solutions.

Troubleshooting

If you encounter issues while setting up or using DDAR and AlphaGeometry, consider the following troubleshooting ideas:

• Ensure that you’ve correctly installed all required dependencies as listed in the repository.
• Double-check that you have the correct weight files for the theorem provers.
• Refer to the official documentation for additional guidance: GitHub Repository.

For more insights, updates, or to collaborate on AI development projects, stay connected with fxis.ai.

Conclusion

By following this guide, you should now be equipped to explore the world of Olympiad geometry using DDAR and AlphaGeometry. It’s an exciting step toward leveraging artificial intelligence in complex problem-solving.

At fxis.ai, we believe that such advancements are crucial for the future of AI, as they enable more comprehensive and effective solutions. Our team is continually exploring new methodologies to push the envelope in artificial intelligence, ensuring that our clients benefit from the latest technological innovations.