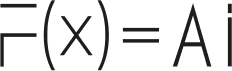If you’re diving into the world of statistics and data visualization, Kernel Density Estimation (KDE) is an essential tool that you cannot overlook. KernelDensity.jl offers a powerful way to estimate the probability density function of a random variable in Julia. Whether you’re dealing with univariate or bivariate data, this guide will walk you through the usage of this package in a user-friendly manner.

Getting Started with Univariate KDE

To kick things off with univariate data, you’ll use the main accessor function kde. Here’s a simple way to construct a UnivariateKDE object from your data:

U = kde(data)

This function accepts keywords that help you customize your KDE:

• boundary: Defines the lower and upper limits of the KDE in a tuple.
• npoints: The number of interpolation points (default is 2048, preferably a power of 2).
• kernel: Specifies the kernel distribution from Distributions.jl (default is Normal).
• bandwidth: Controls the smoothness of the density estimate (default is Silverman’s rule).

Imagine you are painting a landscape; the kernel represents your paintbrush, while the bandwidth is the size of that brush. A wider brush might give you a blurrier view (greater bandwidth), while a finer brush allows for more detail (smaller bandwidth). Choosing the right bandwidth is crucial for achieving the right level of detail in your landscape.

Advanced Univariate KDE Functions

If you want more control over your density estimation, there are related functions such as:

• kde_lscv(data): This version automatically selects bandwidth using least-squares cross-validation.
• kde(data, midpoints::R): Let’s you specify the internal grid while still allowing kernel and bandwidth adjustments.
• kde(data, dist::Distribution): Allows selection of the exact distribution for the kernel.
• kde(data, midpoints::R, dist::Distribution): Combines grid and distribution specifications.

Exploring Bivariate KDE

For two-dimensional data, Bivariate KDE functions mirroring those of univariate estimates are also available. You can pass data as:

B = kde((xdata, ydata))

or in a matrix format:

B = kde(datamatrix)

In this case, optional arguments should also be tuples. For instance:

• boundary: Defined as a tuple of tuples ((xlo,xhi),(ylo,yhi)).

The resulting BivariateKDE object B will provide gridded coordinates and a bivariate density estimate.

Interpolation Made Easy

The KDE objects you create store gridded density values along with their coordinates. However, if you need to interpolate intermediate values, the Interpolations.jl package allows you to do just that:

pdf(k::UnivariateKDE, x)

pdf(k::BivariateKDE, x, y)

To enhance efficiency, especially with multiple calls to pdf, consider creating an intermediate object:

ik = InterpKDE(k) 
pdf(ik, x)

Troubleshooting Tips

If you encounter issues while working with KernelDensity.jl, here are some common troubleshooting tips:

• Problem: The KDE plot looks odd.
  Solution: Check your bandwidth settings. You may need to adjust it for a smoother or more refined output.
• Problem: Data points are outside the boundary limits.
  Solution: Ensure the boundary is set properly in your kde function to encompass all your data points.

For more insights, updates, or to collaborate on AI development projects, stay connected with fxis.ai.

Final Thoughts

At fxis.ai, we believe that such advancements are crucial for the future of AI, as they enable more comprehensive and effective solutions. Our team is continually exploring new methodologies to push the envelope in artificial intelligence, ensuring that our clients benefit from the latest technological innovations.

With this guide in hand, you’re now equipped to tackle kernel density estimation in Julia with confidence. Happy coding!