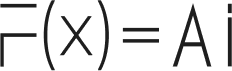Data verification challenges plague organizations handling massive datasets across global networks. Traditional methods require downloading entire databases to verify single records, creating bottlenecks that cripple system performance. However, cryptographic Merkle trees solve this fundamental problem through mathematical elegance and computational efficiency.

Imagine verifying a single transaction among millions without downloading the complete blockchain. Furthermore, picture confirming file integrity in distributed storage systems using minimal bandwidth. These scenarios represent everyday realities where Merkle trees provide transformative solutions for data authentication challenges.

Understanding Merkle Tree Fundamentals

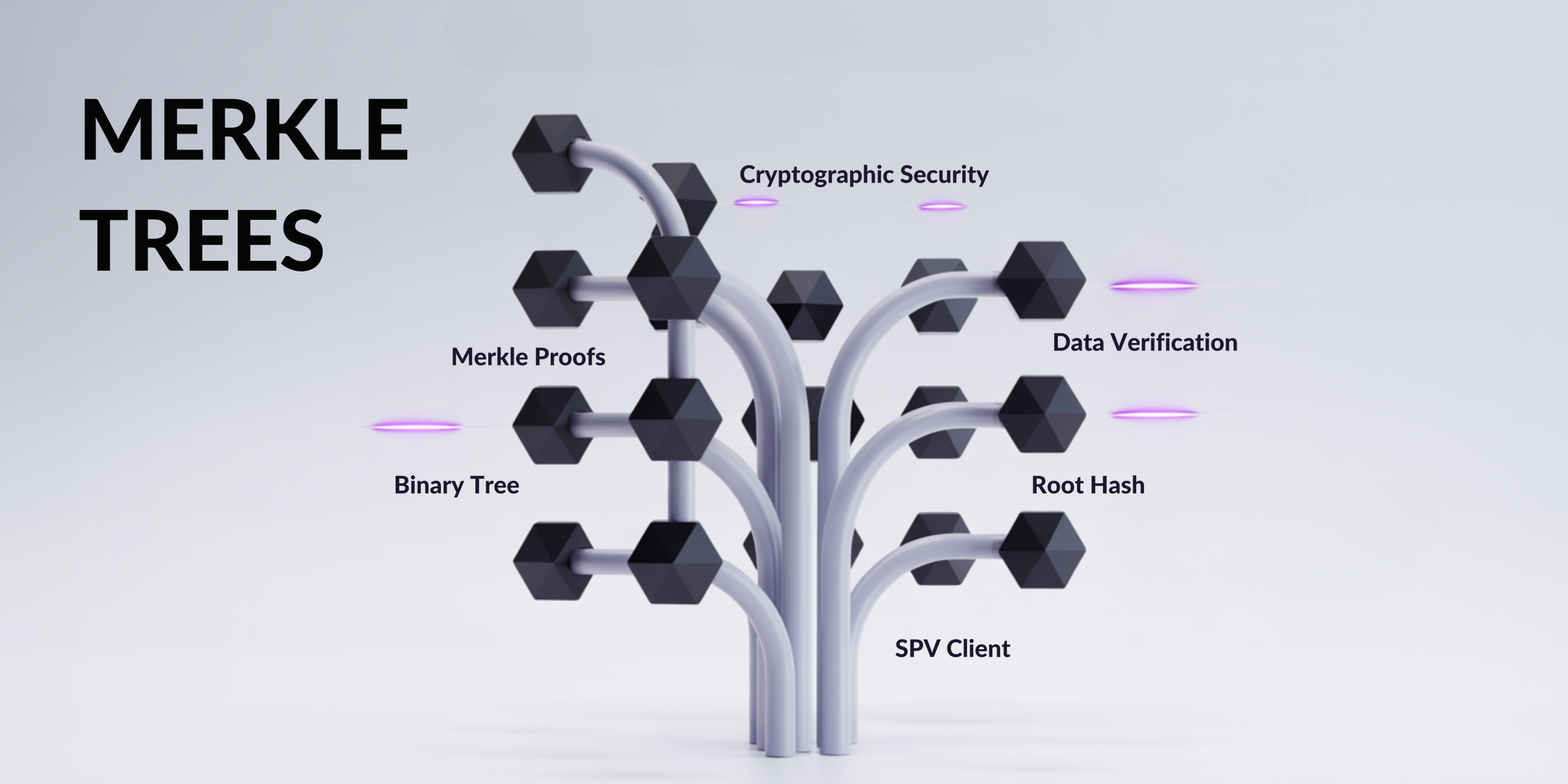
Named after computer scientist Ralph Merkle who introduced them in 1979, Merkle trees represent sophisticated cryptographic data structures that organize information hierarchically. Moreover, they function as binary trees where each leaf node contains a hash of individual data blocks, while parent nodes store combined hashes of their children.

The mathematical foundation relies on cryptographic hash functions that transform arbitrary data into fixed-size strings. Additionally, these functions exhibit avalanche effects where tiny input changes create dramatically different outputs. Subsequently, this property enables tamper detection across entire datasets through single hash comparisons.

Consider a library catalog system managing millions of books. Traditional verification requires checking every record individually. However, Merkle trees enable instant verification of the entire catalog’s integrity through one root hash comparison. Therefore, librarians can detect unauthorized changes without examining individual entries.

The tree structure creates logarithmic verification complexity instead of linear relationships. Consequently, verifying data in million-record databases requires only about 20 hash calculations rather than checking every single record. This exponential efficiency gain transforms how organizations approach large-scale data verification.

Merkle Tree Construction: Binary Tree Building and Hash Calculation

The construction process begins with organizing raw data into individual blocks or transactions. Subsequently, each data block undergoes cryptographic hashing using SHA-256 algorithms, creating unique digital fingerprints that represent the original data.

Step-by-step construction process:

• Divide dataset into equal-sized blocks
• Generate cryptographic hash for each block
• Pair adjacent hashes and combine them
• Create parent nodes from combined child hashes
• Continue until reaching single root hash

During construction, the system pairs leaf nodes and computes their combined hash values. Meanwhile, if an odd number of nodes exists at any level, the algorithm duplicates the last node to maintain binary tree structure. This process continues recursively until only one hash remains at the tree’s apex.

The mathematical elegance lies in the exponential reduction of verification complexity. Therefore, instead of checking thousands of individual data pieces, users can verify integrity through a logarithmic number of hash calculations.

Merkle Root: Summarizing Large Datasets with Single Hash

The Merkle root represents the crown jewel of the entire tree structure. Additionally, this single hash value encapsulates the integrity of all underlying data blocks. Furthermore, any modification to individual data pieces cascades upward, fundamentally altering the root hash.

This characteristic provides powerful tamper-detection capabilities. Subsequently, network participants can quickly verify dataset integrity by comparing Merkle roots. If roots match, the underlying data remains unchanged; otherwise, tampering has occurred somewhere within the structure.

Key advantages of Merkle roots:

• Compact representation of large datasets
• Instant integrity verification
• Efficient storage requirements
• Cryptographically secure authentication

Bitcoin exemplifies practical Merkle root implementation in real-world applications. Specifically, each block header contains a Merkle root representing all transactions within that block. Consequently, light clients can verify transaction inclusion without downloading complete blockchain data.

Merkle Proofs: Efficient Verification Without Full Data

Merkle proofs demonstrate the true power of this cryptographic structure. Moreover, they enable verification of specific data elements without requiring complete dataset access. Additionally, the proof consists of a minimal set of hash values needed to reconstruct the path from target data to the Merkle root.

The verification process involves collecting sibling hashes along the path from leaf to root. Subsequently, the verifier combines these hashes in sequence, ultimately computing the expected root value. If the calculated root matches the known authentic root, the data proves valid.

Proof verification benefits:

• Logarithmic complexity instead of linear
• Minimal bandwidth requirements
• Preserves privacy of unrelated data
• Maintains cryptographic security guarantees

Consider a tree containing 1,000 data blocks. Traditional verification requires downloading all 1,000 pieces. However, Merkle proofs need only about 10 hash values (log₂(1000)) to verify any specific block. Therefore, this represents a 99% reduction in verification overhead.

Simplified Payment Verification (SPV): Lightweight Client Implementation

Simplified Payment Verification transforms how lightweight clients interact with blockchain networks. Furthermore, SPV enables mobile wallets and resource-constrained devices to participate without storing complete blockchain data. Additionally, this approach relies heavily on Merkle tree properties for secure operation.

SPV clients download only block headers containing Merkle roots. Subsequently, they request Merkle proofs for relevant transactions from full network nodes. Meanwhile, this design maintains security while dramatically reducing storage and bandwidth requirements.

SPV implementation advantages:

• Reduced storage from gigabytes to megabytes
• Faster synchronization with network
• Lower computational requirements
• Maintained cryptographic security

The trade-off involves trusting the majority of network nodes regarding transaction validity. However, the cryptographic guarantees ensure that accepted transactions genuinely exist within valid blocks. Consequently, SPV provides an excellent balance between security and resource efficiency.

Modern cryptocurrency wallets extensively utilize SPV principles. Therefore, users can securely manage digital assets without operating full blockchain nodes. This accessibility democratizes cryptocurrency participation across diverse hardware platforms.

Real-World Applications and Benefits

Merkle trees extend far beyond cryptocurrency applications in modern technology ecosystems. Additionally, distributed storage systems like IPFS use Merkle structures for content verification and deduplication. Furthermore, software update systems employ these trees to ensure package integrity during distribution across networks.

Version control systems also benefit significantly from Merkle tree principles. Moreover, Git version control uses similar hash-based structures to track file changes and maintain repository integrity efficiently. Subsequently, developers can verify code history without examining every individual modification. The efficiency gains become more pronounced with larger datasets. Therefore, organizations handling massive data volumes find Merkle trees indispensable for maintaining integrity while minimizing verification overhead.

FAQs:

1. How do Merkle trees improve security compared to traditional checksums?
   Merkle trees provide hierarchical verification that makes targeted tampering extremely difficult. Moreover, any change to individual data automatically invalidates the entire tree structure. Subsequently, attackers cannot modify specific pieces without detection, unlike simple checksum approaches that protect only complete datasets.
2. What happens when the number of data blocks is not a power of two?
   The algorithm handles odd numbers by duplicating the last node at each level. Furthermore, this ensures the binary tree structure remains intact. Additionally, the duplication process doesn’t compromise security since cryptographic hashes make collision attacks computationally infeasible.
3. Can Merkle proofs be forged or falsified?
   Forging Merkle proofs requires breaking underlying cryptographic hash functions. Moreover, with SHA-256 providing 2^256 possible outcomes, successful forgery becomes computationally impossible with current technology. Subsequently, the security relies on well-established cryptographic assumptions.
4. How much storage do SPV clients actually save?
   SPV clients typically reduce storage requirements by 99% or more compared to full nodes. Furthermore, a complete Bitcoin blockchain exceeds 400GB, while SPV clients need only a few hundred megabytes. Additionally, this dramatic reduction enables cryptocurrency access on smartphones and IoT devices.
5. Do Merkle trees work with encrypted data?
   Merkle trees function excellently with encrypted data since they operate on hash values rather than original content. Moreover, encryption adds another security layer without interfering with tree construction. Subsequently, organizations can maintain both confidentiality and integrity verification simultaneously.
6. What are the computational costs of Merkle proof verification?
   Verification requires logarithmic time complexity, typically involving 10-20 hash calculations for datasets containing millions of elements. Furthermore, modern processors handle these operations in microseconds. Therefore, the computational overhead remains negligible even for resource-constrained devices.
7. Can Merkle trees detect which specific data was tampered with?
   While Merkle trees excel at detecting tampering, they don’t directly identify corrupted data locations. However, binary search techniques using multiple Merkle proofs can efficiently locate compromised sections. Subsequently, this approach maintains the logarithmic efficiency while providing diagnostic capabilities.