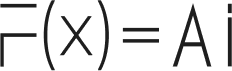Have you ever wondered how programmers solve seemingly impossible problems with elegant, simple code? The answer often lies in recursion programming techniques—a powerful approach that transforms complex challenges into manageable solutions. As someone who’s spent countless hours debugging recursive functions, I can tell you that mastering these concepts will fundamentally change how you approach computer science problems.

Recursion isn’t just a programming trick; it’s a way of thinking that mirrors how we naturally solve problems in real life. Think about Russian nesting dolls—each doll contains a smaller version of itself until you reach the tiniest one. Similarly, recursive solutions work by solving smaller versions of the same problem until reaching the simplest case.

What Makes Recursion So Powerful?

Imagine you’re organizing a company’s file system with thousands of folders and subfolders. Instead of writing complex loops to navigate every possible path, recursion allows you to say: “Process this folder, then do the same for each subfolder.” This approach reduces hundreds of lines of code to just a few elegant statements.

Moreover, recursion programming techniques shine when dealing with naturally hierarchical structures. Whether you’re parsing JSON data, traversing decision trees, or implementing search algorithms, recursion provides clarity that iterative approaches often lack.

Recursive Thinking: Breaking Problems into Smaller Subproblems

The journey to mastering recursion begins with developing recursive thinking—a mental framework that identifies self-similar patterns within complex problems. Rather than being overwhelmed by the problem’s full complexity, you learn to focus on the relationship between the problem and its smaller instances.

• Discovering the Pattern

Successful recursive algorithms start with a crucial question: “How can this problem be expressed in terms of a smaller version of itself?” For example, when calculating the factorial of 5, you realize it’s simply 5 multiplied by the factorial of 4. This insight transforms a multiplication sequence into a recursive relationship.

Consider the classic Fibonacci sequence, where each number equals the sum of the two preceding ones. Instead of tracking multiple variables through loops, recursion lets you express this naturally:
F(n) = F(n-1) + F(n-2). This mathematical elegance translates directly into code that reads like the problem description.

• Building Confidence in Recursive Solutions

Initially, trusting that recursive functions will correctly solve subproblems feels counterintuitive. However, this “leap of faith” becomes second nature with practice. You learn to focus on defining the relationship correctly, trusting that the recursion will handle the rest.

The key insight is recognizing that you don’t need to trace through every recursive call mentally. Instead, verify that your function correctly handles the base case and properly reduces the problem size with each recursive call.

Base Cases: Termination Conditions and Recursion Stopping Points

Every recursive solution requires carefully crafted base cases—the foundation that prevents infinite loops and provides concrete answers for the simplest problem instances. Without proper base cases, your elegant recursive function becomes a stack overflow waiting to happen.

• Identifying the Simplest Cases

Base cases represent the problem instances so simple they require no further recursion. When calculating factorials, the base case typically handles n = 0 or n = 1, returning 1 directly. For binary search algorithms, the base case occurs when the search space becomes empty or contains the target element.

The art lies in identifying all edge cases that could cause problems. Consider a function that processes strings—you need base cases for empty strings, single characters, and potentially null inputs. Each base case should handle a specific scenario that doesn’t require recursive processing.

• Avoiding Common Pitfalls

Many developers focus intensely on the recursive logic while overlooking base case completeness. This oversight leads to subtle bugs that surface with unexpected inputs. Therefore, always test your recursive functions with edge cases, including empty inputs, single-element cases, and boundary conditions.

Additionally, ensure your recursive calls actually progress toward the base case. A common mistake involves recursive calls that don’t reduce the problem size, creating infinite recursion. For instance, calling factorial(n) instead of factorial(n-1) creates an endless loop.

Recursive Calls: Function Self-Invocation and Call Stack Management

Understanding call stack dynamics becomes crucial when working with recursion programming techniques. Each recursive call creates a new execution frame, storing local variables, parameters, and return addresses. This stack-based approach enables the elegant unwinding that produces final results.

• How the Call Stack Works

When a function calls itself, the system doesn’t replace the current execution—it creates a new layer on top. Each layer maintains its own variable space, allowing different recursive levels to work with distinct data. For example, when calculating factorial(5), the stack maintains separate frames for factorial(5), factorial(4), factorial(3), and so on.

This layered approach explains why recursion works: each level solves its piece of the puzzle, then passes the result back to the calling level. The final answer emerges as the stack unwinds, combining results from each recursive call.

• Memory Management Considerations

Deep recursion can exhaust available stack memory, leading to crashes in production systems. Therefore, consider the maximum recursion depth your functions might encounter. Processing a million-element array recursively will likely exceed stack limits on most systems.

For situations requiring deep recursion, consider iterative alternatives or languages that support tail call optimization. Additionally, some problems benefit from converting recursion to iteration using explicit stack data structures, giving you control over memory usage.

Tail Recursion: Optimization Techniques and Stack Efficiency

Tail recursion represents an advanced optimization technique where recursive calls occur as the final operation in a function. This seemingly small change enables significant performance improvements, as optimizing compilers can transform recursive calls into efficient loops.

• Recognizing Tail Recursive Patterns

A function exhibits tail recursion when the recursive call appears as the last statement, and its result is returned directly without additional processing.

Consider this tail-recursive factorial implementation: Instead of multiplying after the recursive call returns, tail recursion accumulates the result through parameters. This approach eliminates the need to maintain stack frames for intermediate calculations.

The Optimization Advantage

Languages supporting tail call optimization can execute tail-recursive functions with constant stack space, effectively converting them to loops behind the scenes. This optimization allows processing arbitrarily large datasets without stack overflow concerns.

However, not all programming languages implement this optimization. JavaScript engines vary in their tail call support, while languages like Scheme guarantee tail call optimization. Therefore, research your target language’s capabilities when designing recursive solutions.

Converting to Tail Recursive Form

Standard recursion often transforms into tail-recursive form using accumulator parameters. This technique shifts computation from the return phase to the parameter-passing phase. For example, instead of multiplying factorial results on return, you maintain a running product as you recurse deeper.

The transformation process involves identifying what calculations occur after recursive calls, then moving those calculations into parameters passed to the next recursive call. This refactoring requires practice but results in more efficient recursive functions.

Real-World Applications and Performance Insights

Recursion programming techniques excel in numerous practical scenarios, from web development to data analysis. Understanding when and how to apply recursion can dramatically simplify complex programming challenges while creating more maintainable code.

• Perfect Use Cases

Tree traversals represent recursion’s natural habitat. Whether navigating DOM elements in web development, processing JSON structures, or implementing database indexes, recursion provides intuitive solutions. The recursive approach mirrors the tree’s structure, making code that’s easy to understand and debug.

Graph algorithms also benefit significantly from recursive implementations. Depth-first search, pathfinding, and connectivity analysis become straightforward when expressed recursively. The recursive calls naturally handle the exploration branching that these algorithms require.

• Balancing Elegance and Performance

While recursion offers conceptual clarity, it may introduce overhead through function call management. Each recursive call involves stack manipulation, parameter passing, and return address storage. For performance-critical applications, profile your recursive solutions against iterative alternatives.

However, don’t automatically assume iteration is faster. Modern compilers optimize recursive calls effectively, and the clarity gained from recursive solutions often outweighs minor performance differences. Focus on correctness first, then optimize based on actual performance measurements.

• When to Choose Iteration Instead

Consider iterative approaches when processing large, flat data structures where recursion depth might exceed stack limits. Additionally, simple counting loops or array processing often benefit from straightforward iteration rather than recursive complexity.

Mathematical computations involving large numbers might also warrant iterative approaches to avoid stack overflow. For example, calculating the nth Fibonacci number for very large n values requires either iteration or memoization techniques to prevent excessive recursive calls.

FAQs:

1. How do I know when a problem is suitable for recursion programming techniques?
   Look for problems with self-similar substructures or hierarchical data. If you can express the problem as “solve this smaller version, then combine the results,” recursion likely provides an elegant solution. Tree structures, fractals, and divide-and-conquer algorithms are classic examples.
2. What’s the most common mistake beginners make with recursive functions?
   Forgetting base cases or creating base cases that don’t actually stop the recursion. Always ensure your recursive calls make progress toward the base case and test with edge cases like empty inputs or single elements.
3. How can I debug complex recursive functions effectively?
   Start by tracing through small examples manually, then use debugging tools to step through function calls. Add print statements to visualize the recursion tree, showing parameters and return values at each level. This approach helps identify where logic breaks down.
4. Is recursion always slower than iteration due to function call overhead?
   Not necessarily. While recursion involves function call overhead, modern compilers optimize recursive calls effectively. Tail-recursive functions with compiler support can achieve performance identical to loops. Focus on code clarity first, then optimize based on actual performance measurements.
5. How deep can recursion go before causing stack overflow?
   This varies by language, system, and available memory. Most systems support hundreds to thousands of recursive calls, but processing millions of elements recursively will likely exceed limits. For deep recursion needs, consider tail recursion optimization or iterative alternatives.
6. Can I convert any recursive function to an iterative one?
   Theoretically, yes. Any recursive function can be rewritten iteratively using explicit stack management. However, the iterative version might become significantly more complex, losing the clarity that made recursion attractive initially.
7. What’s the difference between direct and indirect recursion?
   Direct recursion occurs when a function calls itself directly. Indirect recursion involves multiple functions calling each other in a cycle (A calls B, B calls C, C calls A). Both require careful base case management, but indirect recursion can be harder to analyze and debug.