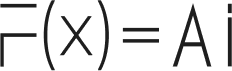In this article, we will explore the fundamental concept of distribution probabilities, especially geared towards the most common distributions utilized in Deep Learning using Python. This tutorial is aimed at everyone from beginners looking to delve into the world of probabilities to seasoned professionals wanting to refresh their knowledge.

Overview of Distribution Probability

When we talk about distribution probabilities, we are discussing how likely different outcomes are for a random variable. It is essential for models where understanding uncertainty is crucial, particularly in Bayesian probability.

The relationship between prior and posterior distributions is important here. If they belong to the same family of distributions, they are called conjugate distributions. This relationship allows for easier computation of posterior distributions using known prior distributions.

From Bayesian probability theory, you can imagine a situation where you have a box of chocolates (prior distribution) and, after tasting some, you adjust your estimate of the total sweetness (posterior distribution) based on your tasting experience. The prior knowledge of the chocolates helps shape your new understanding!

Distribution Probabilities and Features

Here are some common distributions you might encounter when dealing with Deep Learning:

• 1. Uniform Distribution (Continuous)

  The probability is the same across the range [a, b]. It’s like a fair dice roll where each face has an equal chance of landing.

  code for uniform distribution

  

• 2. Bernoulli Distribution (Discrete)

  Used for binary outcomes (success or failure). If you don’t account for prior probabilities, you may end up overfitting your model.

  code for bernoulli distribution

  

• 3. Binomial Distribution (Discrete)

  This distribution concerns finding the number of successes in a series of independent experiments. It accounts for prior probabilities.

  code for binomial distribution

  

• 4. Multi-Bernoulli Distribution / Categorical Distribution (Discrete)

  This expands upon the Bernoulli distribution to more than two outcomes, allowing for greater versatility.

  code for categorical distribution

  

• 5. Multinomial Distribution (Discrete)

  Similar to the categorical distribution, this applies when outcomes can be one of K classes.

  code for multinomial distribution

  

• 6. Beta Distribution (Continuous)

  This is conjugate to both the binomial and Bernoulli distributions, making posterior predictions easy from prior knowledge.

  code for beta distribution

  

• 7. Dirichlet Distribution (Continuous)

  Used as a conjugate prior for the Multinomial distribution; if K=2, it simplifies to a Beta distribution.

  code for dirichlet distribution

  

• 8. Gamma Distribution (Continuous)

  This distribution can represent situations where we are interested in the waiting time until an event occurs. It can relate back to Beta distribution under certain conditions.

  code for gamma distribution

  

• 9. Exponential Distribution (Continuous)

  Dedicated to time until an event, this is a special case of the Gamma distribution when alpha equals 1.

  code for exponential distribution

  

• 10. Gaussian Distribution (Continuous)

  Known as the bell curve, it’s crucial in statistics as it represents a common distribution of data.

  code for gaussian distribution

  

• 11. Normal Distribution (Continuous)

  A standardized form of the Gaussian distribution featuring 0 mean and 1 standard deviation.

  code for normal distribution

  

• 12. Chi-squared Distribution (Continuous)

  Essential in hypothesis testing, this distribution summarizes the variability of data points.

  code for chi-squared distribution

  

• 13. Student-t Distribution (Continuous)

  Sharing properties with the normal distribution but with heavier tails which account for more variability in small samples.

  code for student-t distribution

  

Troubleshooting Ideas

If you encounter issues while working with these distributions, consider the following troubleshooting tips:

• Ensure that the correct libraries are installed and imported in your Python environment.
• Check for any typos in the code that could lead to errors.
• Refer to the documentation for each distribution for parameter requirements.
• Ensure that you are using compatible Python versions and libraries.

For more insights, updates, or to collaborate on AI development projects, stay connected with fxis.ai.

Conclusion

Understanding the relationship between different probability distributions is crucial in the realm of Deep Learning and statistics as a whole. By leveraging the above distributions, you can effectively model uncertainty and make better predictions.

At fxis.ai, we believe that such advancements are crucial for the future of AI, as they enable more comprehensive and effective solutions. Our team is continually exploring new methodologies to push the envelope in artificial intelligence, ensuring that our clients benefit from the latest technological innovations.